Problem

A month ago, I wanted to print a picture. However, I didn’t know how to use GUI programs like LibreOffice or GIMP to print images with their actual size. I know that this can be easily done in M$ Paint.¹

Nonetheless, as a free software supporter, I should refuse using proprietary softwares and seek free alternatives.

A month ago, I took a test and was asked whether “a group of 689 elements is closed under the group operation”. The question is trivial, but one can discover another question: Does such a group exists?

In order to “proceed with with my work”, I temporarily accepted the existence fo swuch a group during the test. However, even though I got the question right and earned some marks for that, I didn’t think that this is true mathematics. To say that one knows this quoted statement, one has to follow the “international standard” of a group and make rigourous arguements from the “basic laws” to prove the existence of such a group.

Thinking that the group of 689 elements isn’t useful, I put that problem aside. After a fortnight, I came up with an answer: $\Z_{13} \times \Z_{53} \cong \Z_{689}$.

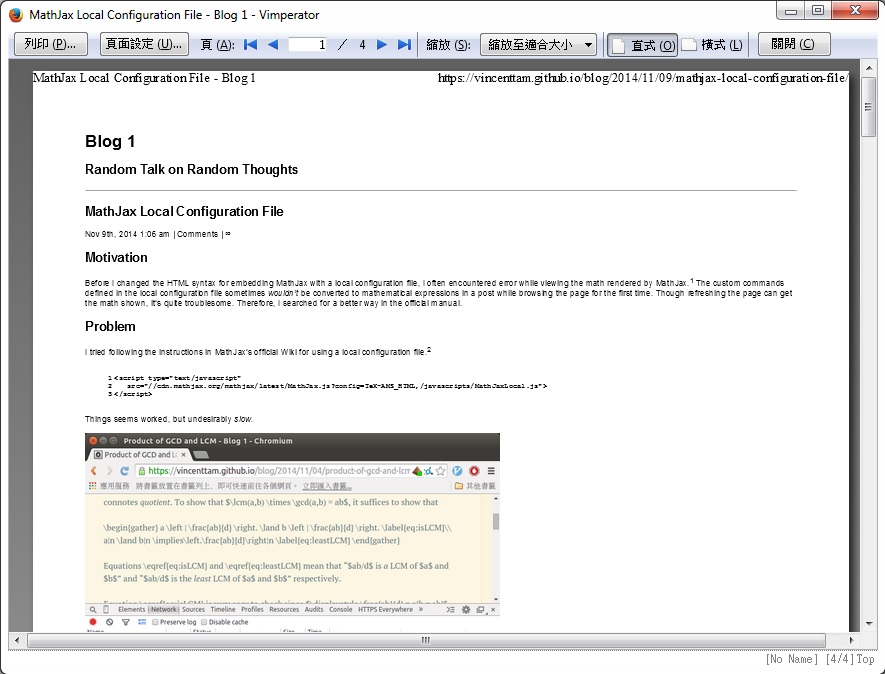
Half a month ago, I didn’t know how to find $\lim\limits_{n \to \infty} \sqrt[n]{a^n+b^n}$. With the help from others, I could show that the answer was $\max\left\{ a,b \right\}$. This inspired me to solve a question which had been in my mind since I was F.3.

Suppose that $M_n (a_1,\dots,a_k) := \sqrt[n]{\frac1k \sum\limits_{i=1}^{k} a_i^n} \quad\forall\,n \in \N$, and $a_i > 0\quad\forall\,i \in \{1, \dots,k\}$. Show that $\lim\limits_{n \to \infty} M_n (a_1,\dots,a_k) = \max\limits_{i \in \{ 1,\dots,k\}} a_i$ and $\lim\limits_{n \to -\infty} M_n = \min\limits_{i \in \{1,\dots,k\}} a_i$.

Proof:

I'll use the facts that $\lim\limits_{n \to \infty} b^{1/n} = 1 \quad\forall\,b>0$. (It can be proved by dividing $b$ into $0 < b < 1$ and $b > 1$. For $b > 1$, let $b^{1/n} = 1 + \delta_n$ for some $\delta_n > 0$. It's a good exercise on the definition of limits, the binomial expansion and elementary properties of inequalities.)

Let $M := \max\limits_{i \in \{1,\dots,k\}} a_i$. Note that

Therefore, taking limit as $n \to \infty$ and applying the Squeeze Theorem, one has

I wrote similar arguments for the case $n \to -\infty$, but after I read Wikipedia, I’ve learnt a quicker way to finish the question.

Replace $a_i$'s with $1/a_i$'s. Then

Hence, $\lim\limits_{n \to -\infty} M_n (a_1,\dots,a_k) = \lim\limits_{n \to -\infty} \sqrt[n]{\frac1k \sum\limits_{i=1}^{k} a_i^n} = \min\limits_{i \in \{1,\ldots,k\}} a_i$.

Googling “tikz tutorial”, one can find several useful PDF documents which are easy to follow, such as the first two results.

1. PGF/TikZ - Graphics for $\rm \LaTeX$ —A tutorial by Meik Hellmund
2. A very minimal introduction to TikZ by Jacques Crémer

The second PDF document covers plotting graphs in rectangular coordinates. How about polar coordinates?

It’s easy to find a solution online, but understanding the code and adapting them according to your needs are much harder. One has to make use of “cs”, which stands for “coordinate system”. If one is too lazy to read more webpages, then one may use the code below.

When I drew figures with TikZ a recent post on limits of composite functions on $\R^n$, I found a way to construct random region with TikZ in a $\rm \TeX$–$\rm \LaTeX$ Stack Exchange question.¹ This inspired me to come up with the following graph.

Output

Source code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

\documentclass[tikz]{standalone}
\begin{document}
\begin{tikzpicture}
  % drawing grid lines
  \foreach \r in {1,...,6} {\draw (0,0) circle (\r);}
  \draw (-6.5,0) -- (6.5,0);
  \foreach \theta in {15,30,...,165} {\draw (\theta:6.5) -- (\theta+180:6.5);}
  % labelling them
  \foreach \r in {2,4,6} {\node[below left] (lbl\r) at (\r,0) {\r};}
  \foreach \t in {0,30,...,330} {
    \node [draw,fill=white] (lbl\t) at (\t:7) {$\theta = \t^\circ$};
  }
  % graph of $r = 5 - \sin(3\theta)$
  \draw[red,ultra thick,smooth cycle,samples=200,domain=0:359]
  plot (\x:{5-sin(3*\x)});
  \node at (270:8) {The graph of $r = 5 - \sin(3\theta)$};
\end{tikzpicture}
\end{document}

• I got the idea of for loop in TikZ from TikZ and PGF Manual.
• I learnt the syntax for plotting functions from the PDF in item (2).

Goal

Same as the one in My CSS Settiings for Printing (1).

Problem

Having written a post on loading MathJax with a local configuration file, I previewed the print layout, saw that the font size was too small.¹

Motivation

Before I changed the HTML syntax for embedding MathJax with a local configuration file, I often encountered error while viewing the math rendered by MathJax.¹ The custom commands defined in the local configuration file sometimes wouldn’t be converted to mathematical expressions in a post while browsing the page for the first time. Though refreshing the page can get the math shown, it’s quite troublesome. Therefore, I searched for a better way in the official manual.

Problem

I tried following the instructions in MathJax’s official Wiki for using a local configuration file.²

1
2
3
4
5

<script type="text/javascript"
	src="//cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS_HTML,
	/javascripts/MathJaxLocal.js
">
</script>

Things seems worked, but undesirably slow.

It took about 16 seconds for loading the math. How can they load quicker with a local configuration file, like http://drz.ac?

Problem

I suddenly found that the Gravatar in my GitHub user profile had disappeared.

Failed attempt

I then went to GitHub to upload the icon.

I googled the red error message, and read the last reply in this thread. Then, I had taken the above screenshot and started a new post on this issue.

Result

Before I finished this post, the Gravatar was back again.

Lessons learnt

As not being a student/worker in IT, I shouldn’t spend much time on developing tools and finding a good solution to a strange problem. Instead, I should use others’ tools to save time and tolerate some faults, as long as I get the job done. Developers will work on the code to improve things later.

Problem

Let $\mathcal{U}$ and $\mathcal{V}$ be open subsets of $\R^n$ and $\R^m$ respectively, $f:\mathcal{V} \to \R^k$ and $g:\mathcal{U} \to \R^m$ be functions such that $g(\mathcal{U}) \subseteq \mathcal{V}$, and $\vect{x}_0 \in \mathcal{U}, \vect{y}_0 \in \mathcal{V}$, and $\vect{z}_0 \in \R^k$ be points such that $\lim\limits_{\vect{x} \to \vect{x}_0} g(\vect{x}) = \vect{y}_0$ and $ \lim\limits_{\vect{y} \to \vect{y}_0} f(\vect{y}) = \vect{z}_0$.

Is it possible that $\lim\limits_{\vect{x} \to \vect{x}_0} f(g(\vect{x})) \ne \vect{z}_0$?

Problem

For sequences of numbers, limit inferior and limit superior are defined as $\liminf (a_n):=\sup\{\inf\{a_k \mid k \ge n\}\}$ and $\limsup (a_n):=\inf\{\sup\{a_k \mid k \ge n\}\}$ respectively; for sequences of sets, they are defined as $\bigcup\limits_{n=1}^{\infty} \bigcap\limits_{k=n}^{\infty} A_k$ and $\bigcap\limits_{n=1}^{\infty} \bigcup\limits_{k=n}^{\infty} A_k$ respectively.

Why are they consistent?

In ProofWiki’s first proof, it has taken me some time to understand. I often write $d=\gcd(a,b)$, $a=a’d$, $b=b’d$ for some $a',b' \in \Z_{>0}$, and $n$ as any common multiple of $a$ and $b$. Then $n = q_1 a = q_2 b$ for some $q_1,q_2 \in \Z$. The letter $q$ connotes quotient. To show that $\lcm(a,b) \times \gcd(a,b) = ab$, it suffices to show that

Equations \eqref{eq:isLCM} and \eqref{eq:leastLCM} mean that “$ab/d$ is a LCM of $a$ and $b$” and “$ab/d$ is the least LCM of $a$ and $b$” respectively.

Equation \eqref{eq:isLCM} is very easy to check since $\displaystyle \frac{ab}{d} = a’b = ab’$.

By Bézout’s Identity, $ax+by=d$ for some $x,y \in \Z$.

Since what we want is $\displaystyle \frac{ab}{d} (\dots) = n$, we multiply both sides of the above equation by $\displaystyle \frac{n}{d}$.

Hence \eqref{eq:leastLCM} is proved.