Tonight, I just go to Facebook as usual, and I’ve just received an error saying that “server not found” in Firefox. The screenshot below illustrates the problem.
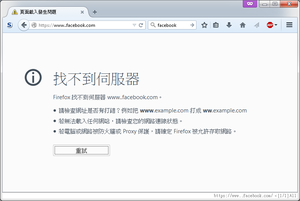
Tonight, I just go to Facebook as usual, and I’ve just received an error saying that “server not found” in Firefox. The screenshot below illustrates the problem.

Lower limit topology ($\R_l$)
K-topology ($\R_K$)
Consider a base element $[a,b)$. At the point $a$, no open interval $(c,d)$ containing $a$ is a subset of $[a,b)$.
Let $B_2 = (-1, 1) - K$. At $B_2 \notin \R_l$ because any base element $[0,b)$ containing 0 must hit $1/n$ for some $n \in \Z_+$ by Archimedean Property of $\Z_+$. Thus, $\forall b > 0, [0,b) \nsubseteq B_2$.
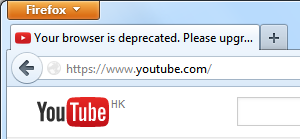
I went to YouTube with the old version Firefox.
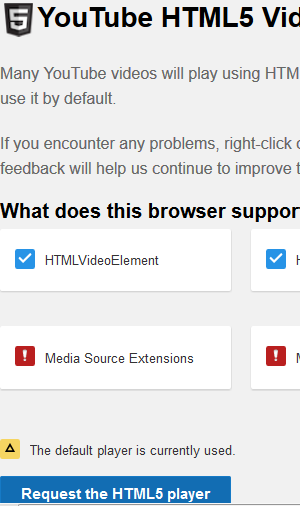
Request YouTube’s HTML5 player and enjoy watching videos.
Just like *nix, <Alt-PrtSc> can be used for capturing only the
current window instead of the whole screen.
When I was a high school student, it’s hard for me to imagine a product whose index looped through all prime numbers because primes don’t appear in a regular way: between 1 and 100, there’re 25 primes, but between 900 and 1000, there’re 14.
Even though it’s easier to imagine the infinite sum whose $n$-th term is $n^{-s}$, without learning the $p$-Test and the Comparison Test for the convergence of infinite sums, I couldn’t understand why the infinite sum in the following equality exists.
I think that the last item is the trickiest step. Writing the following lines, I understood this equation.
Steps \eqref{step1} (resp. \eqref{step3}) holds because for each $k^{-s}$ in the leftmost bracket, powers of 2 (resp. 3) can be taken out from $k$. In steps \eqref{step2} and \eqref{step4}, the formula for the sum of geometric series is applied.
I’ll end this post by wrapping up the above ideas by summation and product signs.
I sometimes upload pictures for illustrating ideas. You may see Two Diagrams Illustrating the Isomorphism Extension Theorem in this blog for example.
Enable users to adjust the size of SVG graphics.
In the linked post, if the zoom level is too large, then part of the image will be hidden.
This is quite inconvenient for users who want a whole picture.
To set up a slide bar which controls the size of an SVG image.
Image size: 200
This is just a small table listing some differences between fbi and fim.
| Advantages | Disadvantages | |
|---|---|---|
| fbi | support SVG files | doesn’t support tmux doesn’t have full control over the zooming size |
| fim | support tmux support custom zooming1 |
doesn’t support SVG files |
To view SVG images in tmux buffers, one can use ImageMagick’s
convert command.2
While writing the above table, I ran into the problem of a Markdown
table with more than one line. Luckily, searching “kramdown table
lines” on Google, I quickly found a Stack Overflow question which
solved my problem.3 Note that <br> is not the best
way: add a slash / to suppress the following messages.
Warning: The HTML tag 'br' on line 15 cannot have any content -
auto-closing it
Warning: The HTML tag 'br' on line 17 cannot have any content -
auto-closing it
Warning: The HTML tag 'br' on line 1 cannot have any content -
auto-closing it
Warning: The HTML tag 'br' on line 1 cannot have any content -
auto-closing it
By :nn% ↩
By convert in.svg out.jpg ↩
Newline in markdown table? on Stack Overflow. ↩
I copied lines from an enumerated list in this blog and pasted it to Vim. The content in each list item was seen in the current Vim buffer, but not the numbers.
A sample ordered list with 2015 items
…
What is seen in Vim after copy and paste
Item one
Item two
Item three
...
Item 2015
If one writes in Markdown and he/she copies a numbered list from elsewhere to a text editor, then it will be very inconvenient to manually add back the numbers. To exaggerate this inconvenience, I put “2015” above.
Insert the item number at the beginning.
1. Item one
2. Item two
3. Item three
...
2015. Item 2015
Last Friday, I had to submit a homework which required me to evaluate $\Pr(A > B)$ and $\Pr(A = B)$, where $A$ and $B$ were two independent Poisson random variables with parameters $\alpha$ and $\beta$ respectively.
I then started evaluating the sum.
Then I was stuck. I couldn’t compute this sum also.
I googled for a solution for hours, and after I saw equation (3.1) in a paper, I gave up finding exact solutions.1 As a supporter of free software, I avoided using M$ Ex*, and wrote a program in C++ to approximate the above probabitities by directly adding them term by term.
Assume that Poisson r.v. A and B are indepedent
Parameter for A: 1.6
Parameter for B: 1.4
Number of terms to be added (100 <= N <= 1000): 8
P(A > B) = 0.423023, P(A < B) = 0.335224, P(A = B) = 0.241691
A one-line method for writing the content of a function which returns the factorial of a number.
Evaluation of a function inside GDB
Keller, J. B. (1994). A characterization of the Poisson distribution and the probability of winning a game. The American Statistician, 48(4), 294–298. ↩
There is an easy way of calculating the volume of $\{(x,y,z) \in \R^3 \mid 0 \le x,y,z \le t, x + y + z \le t\}$: just consider the permutation of $x,y,z$.1 This can be easily generalized to $n$ dimension.
To calculate its centre of mass.
By symmetry, we conclude that the center of mass is $\left(\frac{t}{n + 1}, \frac{t}{n + 1}, \ldots, \frac{t}{n + 1}\right) \in \R^n$.
Simplex. (2015, March 29). In Wikipedia, The Free Encyclopedia. Retrieved 15:34, April 6, 2015, from http://en.wikipedia.org/w/index.php?title=Simplex&oldid=654074423 ↩
If one assumes that servers $X_1$ and $X_2$ has exponential service times with rate $\lambda_1$ and $\lambda_2$ respectively, (i.e. $X_i \sim \Exp(\lambda_i), i = 1,2$), then one can follow the standard arguments and say that the waiting time $\min\left\{ X_1, X_2 \right\} \sim \Exp(\lambda_1 + \lambda_2)$, so the expected waiting time is $1/(\lambda_1 + \lambda_2)$.
I tried finding the expected waiting time by conditioning on $X_1 - X_2$.
Similarly, one has $\Pr(X_1 \le X_2) = \lambda_1/(\lambda_1 + \lambda_2)$.
This is different from what we expect. What’s wrong with the above calculation?
I really thought about the meaning of $\E[\min\left\{ X_1, X_2 \right\} \mid X_1 > X_2]$, and find out that this conditional expectation won’t be helpful because
Actually, one can divide it into two halves.
By observing the symmetry between the subscripts ‘1’ and ‘2’ in the above equation, we only need to evaluate one of them.
Similarly, one has
Substitute \eqref{eq:half_int} and \eqref{eq:half_int2} into \eqref{eq:head}.
This is consistent with what we expect. I finally understand what’s wrong in \eqref{eq:wrong}: $X_1$ isn’t independent from $X_1 - X_2$.
By induction, we can generalize \eqref{eq:fin} to the expected waiting time for $n$ servers in parallel: if $X_i \sim \Exp(\lambda_i) \,\forall 1 \le i \le n$, then