Background

I changed my way of writing block equations for RSS.¹ However, in my old post about the Contraction Mapping Principles, there’s an inequality on the rate of convergence of a point in a complete metric space to the unique fixed point of the Lipschitz mapping with a Lipschitz constant strictly less than one.²

\[ \begin{aligned} d(x^*,x_n) =& d\left( \lim_{k \to \infty} x_k,x_n\right) \\\
=& \lim_{k \to \infty} d(x_k,x_n) \\\
\le& \lim_{k \to \infty} \frac{q^n}{1 - q} d(x_1,x_0) \\\
=& \frac{q^n}{1 - q} d(x_1,x_0) \end{aligned} \]

1
2
3
4
5
6
7
8
9

\\[
\begin{aligned}
d(x^\*,x\_n) =& d\left( \lim\_{k \to \infty} x\_k,x\_n\right) \\\\\\\\
=& \lim\_{k \to \infty} d(x\_k,x\_n) \\\\\\\\
\le& \lim\_{k \to \infty} \frac{q^n}{1 - q} d(x\_1,x\_0) \qquad
  \text{(by \eqref{eq:finite_err})} \\\\\\\\
=& \frac{q^n}{1 - q} d(x\_1,x\_0)
\end{aligned}
\\]

Starting from the second line in the above block equation, at the left of the binary relation symbols there’s a whitespace character.

Motivation

In the past, I used double dollar signs $$ to enclose block equations. As a result, readers couldn’t see them in Firefox.

How can these missing parts be put back to the RSS feeds?

I’ve found a list of $\rm \LaTeX$ commands for Greek alphabets. Unluckily, when I right-clicked each alphabet, the popped-up menu could only show the MathML code, but not the $\rm \LaTeX$ code. Therefore, I have to use MathJax’s previewer to verify the commands.

Searching symbols in CTAN’s Comprehensive $\rm \LaTeX$ Symbol List is time-consuming. For example, when I was writing my previous post about groups, I made use of angle brackets and the ‘$\circ$’ symbol for composition of two functions. At first, I typed < and >, but they didn’t look good. In fact, one should use ‘$\langle$’.¹ How can one find the commands for those characters? Detexify is the answer for commonly used symbols.

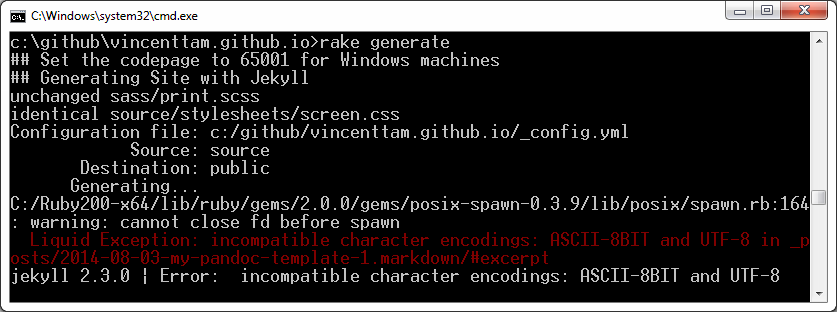
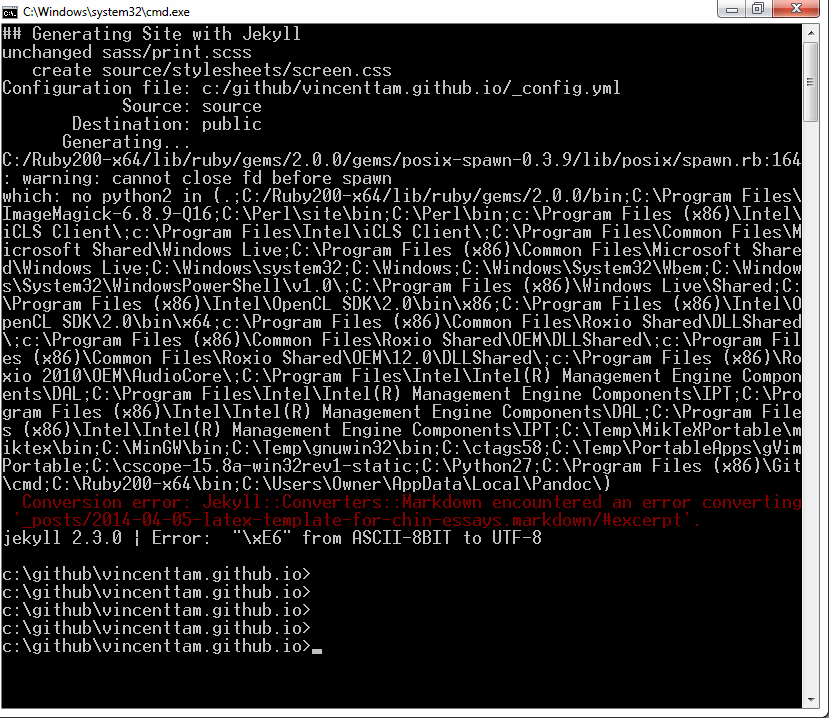
Half a year ago, when I heard the concept of well-defined functions, I wasn’t familiar with it.

I’ve just worked out a problem, and got more idea about that concept. The problem should be quite easy. It asks readers to show that if $\langle G, * \rangle$ is a group, $g \in G$ and $\varphi_g: G \to G$ is a mapping defined by $\varphi_g (x) = g * x * g^{-1}$, then $\varphi_g: G \to G$ is an automorphism. However, I misunderstood the wordings in the question, and attempted to prove that the binary structure $\langle \{\varphi_g \mid g \in G\},\circ \rangle$ is isomorphic to $\langle G, * \rangle$, where $\circ$ denotes the composition of functions. As a result, I let $\phi: \{\varphi_g \mid g \in G\} \to G$ be a mapping defined by $\phi(\varphi_g) = g$. The associativity, existence of identity element and existence of inverse of the binary structure can be easily verified. By the very definition of $\phi$, it seems that its surjectivity is very obvious. I continued to write “injectivity of $\phi$ is also obvious.”

\[ \phi(\varphi_{g_1}) = \phi(\varphi_{g_2}) \iff g_1 = g_2 \implies \varphi_{g_1} = \varphi_{g_2} \]

I tried to turn the above rightward double arrow ‘$\implies$’ into a double-headed one. If I couldn’t do so, it means that $\phi(\varphi_{g_1}) = \phi(\varphi_{g_2})$, though $g_1 \neq g_2$. I realised that I need to check whether $\phi$ was well-defined. As a result, I wasted an hour on some equations. Suddenly, I stopped substituting $x = g_1$ or $x = g_2$ into $\varphi_{g_1} (x) = \varphi_{g_2} (x)$. Instead I took $\langle G, * \rangle = \langle \R, \cdot \rangle$ and realized what I just did was a waste of time.

The following axioms seem to be weaker.

Let $G$ be a set, and $*: G \times G \to G$ be a binary operation.

Associativity

$\forall a,b,c \in G, (a * b) * c = a * (b * c)$

Existence of left identity

$\exists e \in G \text{ s.t. } \forall a \in G, e * a = a$

Existence of left inverse

$\forall a \in G, \exists a^{-1} \in G \text{ s.t. } a^{-1} * a = e$

Claim: They’re actually equivalent definition of a group.

Tonight, I worked on my blog. Here’re something done.

1. Fixed a dead link in Using Octopress on Another Device in Blog 1.
2. Fixed url in _config.yml: it should be in lower case.¹
3. Understand item 5 of Scott Cheng’s post on setting up Octopress.² In May, I didn’t understand it.³ I’ve tested it in order to understand what it really means. After running rake setup_github_pages, _deploy folder has only local master branch, and no remote branch. Therefore, it’s impossible to remote the only branch there. To avoid conflicts when I push my commits on master branch to my remote repository in GitHub, I ran some commands as shown below.
4. Fixed the network graph of the GitHub repository for Blog 1.
   • Original graph: Due to my poor knowledge on Git, master branch shares, as shown in the graph, a common node with source branch. This is wrong!
   • Deleted locally origin/master branch and master branch in the remote repository to clear the mess.
   • In the new graph, those two branches don’t share a common node anymore.

[owner@localhost ~/octopress/_deploy]$ git branch -rd origin/master
Deleted remote branch origin/master (was e745caf).
[owner@localhost ~/octopress/_deploy]$ git branch -a
* master
[owner@localhost ~/octopress/_deploy]$ git push origin --delete master
To git@github.com:vincenttam/vincenttam.github.io.git
 - [deleted]         master

Background

In *nix, one can use :Gcommit to commit the staged changes, provided that fugitive.vim has been installed.

Problem

How can one use the Vim plugin within Vim on M$ Win*?

Discussion

Inspired by a Stack Overflow question, I set my core.editor to gvim -f through git config.

Then I tried running git commit in , but it’s “aborting commit due to empty commit message”.

Why is the -f flag there? It’s because the --nofork option causes gVim to be in the foreground in *nix. I’ve learnt this from GitHub. The -w flag in the commands for setting other editors as the default editor for Git is the key for the above quoted message.

I tried to solve this problem by reading Vim’s offical manual about nofork, and it’s clearly stated that this option wasn’t supported in M$ Win* unless I’m “running it with an installed … gvim.bat”.

To conclude, if I’m working on M$ Win*, I’ll just forget about :Gcommit in Vim, and use .

Problem

Background

This Sunday, I tried to do something similar to what I did in May—install Octopresss on Windows 7.¹ Different from last time, I used Ruby 2.0.0, the newest version of RubyInstaller for Windows that I could find.²

I could use Octopress with Ruby 1.9.3, so I expected that I could easily deploy things with Ruby 2.0.0. However, I was mistaken.

Problem